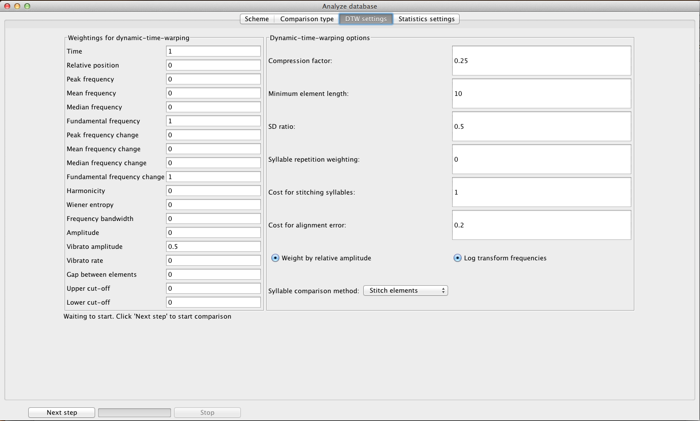
The screen above is reached by selecting “Computer comparison by dynamic time warping” from the second Analysis window.
A common task in bioacoustic studies is to compare signals. The underlying question may be “are these two signals the same or are they different?” Alternatively, it may be more general: “how different are these two signals?” Computational comparisons allow these questions to be answered for large datasets in a repeatable way.
The limitations of computational comparison of sounds are perhaps less obvious than the benefits. Vocal signals are time series. As such, there is no objectively ‘best’ way to decide how to align them (e.g. how to penalize stretching or compression of a signal). Dynamic time warping uses a simple dynamic programming technique to search for an optimal alignment of two signals. The algorithm then calculates a dissimilarity score between two signals based on provided parameters along this alignment. This is an established algorithm that works reasonably well over a wide-range of conditions. The implementation used in Luscinia is further optimized by using interpolation between points to optimize scores for rapidly modulated signals.
The user must decide which acoustic features to use in the analysis. These options are shown in the left panel above, and correspond to the parameters measured for every element in the Spectrogram (see the Parameters window for more details). Note that these parameters refer to vectors of measurements, not single points. ‘Peak frequency’ refers to the peak frequency at each time point in an element, not the overall peak frequency of the element.
The choice of which parameters to use is not an objective one, at this stage of our scientific knowledge. Ultimately, it would be better to base this decision on our knowledge of signal perception or production. Nevertheless it seems safe to say that any comparison should probably include Time and a frequency measure (which frequency measure to use depends on the signal. Peak frequency is very different from fundamental frequency in harmonically structured signals like zebra finch songs.) Measures of frequency change are also likely to be broadly informative, and may even replace absolute frequency in certain situations. They provide more information about the form of an element. While the frequency measures can be regarded as akin to ‘Absolute pitch’, the frequency measures are more related to ‘Relative pitch’.
The use of the other parameters, such as measures of noisiness and broad-bandedness (Wiener Entropy, Harmonicity and Bandwidth), or vibrato still depends on the intuition of the experimenter. One system is to rely on variation in the database. If there is little variation in noisiness, then it is better not to use those parameters in the analysis.
In the DTW analysis, each parameter is normalized according to three factors: the first two are the standard deviation of that parameter over the whole dataset, the standard deviation of the individual pair of songs that are being compared. The weighting of these two is controlled by the SD ratio parameter. A value of 0 weights entirely on population-level standard deviation, while 1 weights entirely on the pairwise variation. When you set SD Ratio to 0, short notes will tend to be clustered more tightly than long notes. When you set SD Ratio to 1, all ‘flat’ tonal elements (elements with no frequency modulation) will tend to be equally dissimilar to each other, no matter their relative frequencies. It is therefore normally better to set SD Ratio to a value between 0 and 1. 0.5 provides good results over a range of conditions.
The third normalizing factor is the weighting of each parameter, which is set by the user on the left hand side of the panel (essentially, the combined standard deviation is divided by this parameter). Parameters are selected by setting their weighting to >0. In most conditions, it is most parsimonious to set parameter weightings to 1 for the parameters you wish to use, at least to begin with.
The right hand side of the panel has a list of parameters, in addition to SD Ratio:
Compression factor: sets how much elements are compressed. If it is set to 1, the data used by the DTW are the measurements at each time step in the spectrogram. If it is 0.25 (for example), the algorithm divides the element length by 4, and averages four measurement points at a time to generate the input dad for the DTW.
Minimum element length: sets a limit to compression. If compression leads to an element shorter than this number of points, then the element length is set to this length instead (if the element was in the first place shorter than the Minimum element length, it is left intact). Note that ‘length’ here means the number of measurement points, not length in terms of time.
These two parameters effect both the speed and the outcome of the comparison. Setting a compression factor <1 can damp some of the noise in measurements, and is a good idea if signals are noisy. If Compression factor is low, and Minimum element length high, this has the effect of making elements in the comparison similar to each other in the number of data points. This influences the comparison of syllables if done by ‘Stitching Elements’ (below), since it increases the relative importance of shorter elements within a syllable.
Syllable repetition weighting: many phrases consist of syllables repeated a number of times. The number of repetitions is not normally taken into account in the dew analysis. By setting this parameter >0, it is. The absolute difference in the log of number of syllable repetitions, for each pair of syllables, is calculated. It is normalized by the standard deviation of log syllable repetitions, the standard deviation of syllable dissimilarities calculated by the DTW, and this weighting parameter. Then it is added to the syllable dissimilarities.
Cost for stitching syllables: if syllable dissimilarities are calculated both by both syllable stitching AND by element to element calculation (see Syllable comparison method below), this parameter, normalized by standard deviation is added to the stitched syllable dissimilarities, before the two measures are combined.
Cost for alignment error: if syllable dissimilarities are calculated by Individual elements (see Syllable comparison method below), this parameter weights the penalty applied when two syllables do not have the same number of elements, or if the optimal alignment of elements in the two syllables involves a shift in order (e.g. the first element in syllable A best matches with the second element in syllable B and so on). The value is relative to the standard deviation in element dissimilarity scores.
Weight by relative amplitude: this weights the DTW score by giving more weight to louder parts of the element. This is useful especially when measurements are less precise for quiet parts of the signal.
Log transform frequencies: this takes the logarithm of frequency parameters before carrying out the DTW analysis. Models of vertebrate sound perception tend to find that perception of frequencies is approximately logarithmic (see e.g. octaves in human music).
Syllable comparison method: Three options are available: Individual elements, Stitch elements, and both. With Individual elements, the DTW dissimilarities between the pairs of elements in two syllables are combined to create an overall dissimilarity score. This method has the advantage of weighting each element equally in the comparison, but involves setting an alignment error penalty (above). It works best when elements are unambiguously defined (e.g., if there is always a clear gap between elements). In many cases, however, elements are clearly separated in one rendition of a syllable, but not in another rendition of the syllable. In this case, very similar syllables can be scored as being very different using the Individual element method. The stitch syllables method solves this problem by first ‘stitching’ together the elements within a syllable and then carrying out one DTW comparison for the whole syllable (making the entire syllable one long element). If there are gaps between elements, this is reflected in the DTW if the parameter ‘time’ is selected. For example, the end of one element and the beginning of the next might produce time parameter scores as follows:
…78, 79, 80, 81, 81, 101, 102, 103, 104, 105, 106…
Syllable stitching therefore effectively deals with segmenting errors. On the other hand, it weights long elements as more important in the comparison. This can lead to errors when a short element is deleted or inserted into an element. Two syllables that appear quite different to the eye may still be ranked as quite similar under the stitch syllables method. One solution to this problem, if it arises, is to set Compression factor quite low (e.g. 0.1), and Minimum element length quite high (e.g. at the same average length as the shorter elements in the data set).
